Lernauftrag 11: Spannungs- und Widerstandsdreieck
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
Eine Spule besteht aus Draht, welcher aufgewickelt ist. Somit besitzt eine Spule zwei Eigenschaften. Zum einen die Induktivität \(L\) und zum Anderen den Widerstand \(R\) des Drahtes selbst. Eine Spule kann also als die Reihenschaltung eines Wirkwiderstand \(R\) und eines Blindwiderstands \(X_L\) dargestellt werden.
Im Zeigerbild stehen Wirkwerte und Blindwerte immer senkrecht zueinander.
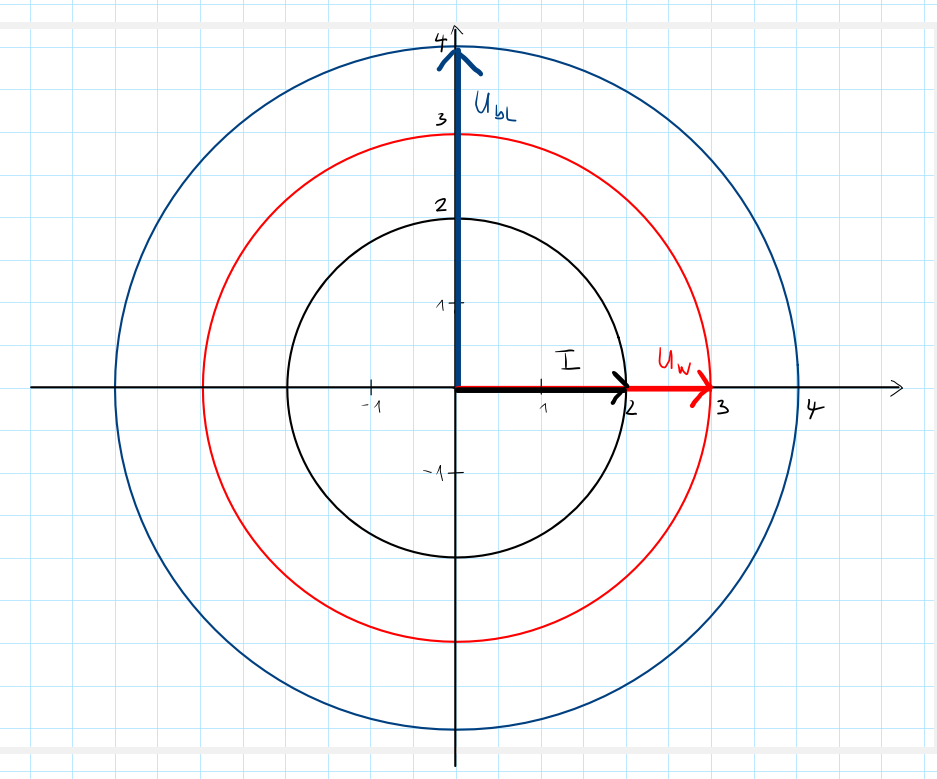
Zeichne ein Zeigerbild. Der Strom \(I=2\ A\) soll auf der X-Achse liegen. Zeichne die Wirkspannung \(U_W=3\ V\) und die induktive Blindspannung \(U_{bL}=4\ V\) ein. Nutze einen geeigneten Maßstab für Strom und Spannung. Nutze die LUCI-Regel um herauszufinden, wie die Spannungszeiger zum Stromzeiger stehen.
Aufgabe 2
Aus dem in Aufgabe 1 gezeichneten Zeigerbild läßt sich ein Spannungsdreieck ableiten. Ermittle wie aus einem Zeigerbild ein Spannungsdreieck gezeichnet werden kann und zeichne das Spannungsdreieck zu deinem Zeigerbild und miss die resultierende Hypotenuse deines Dreiecks. Diese stellt die Gesamtspannung \(U\) dar.
Ausgehend vom Zeigerbild verschieben wir den Vektor (Pfeil) von \(U_{bL}\) so, daß er am Ende des Vektors \(U_W\) beginnt:
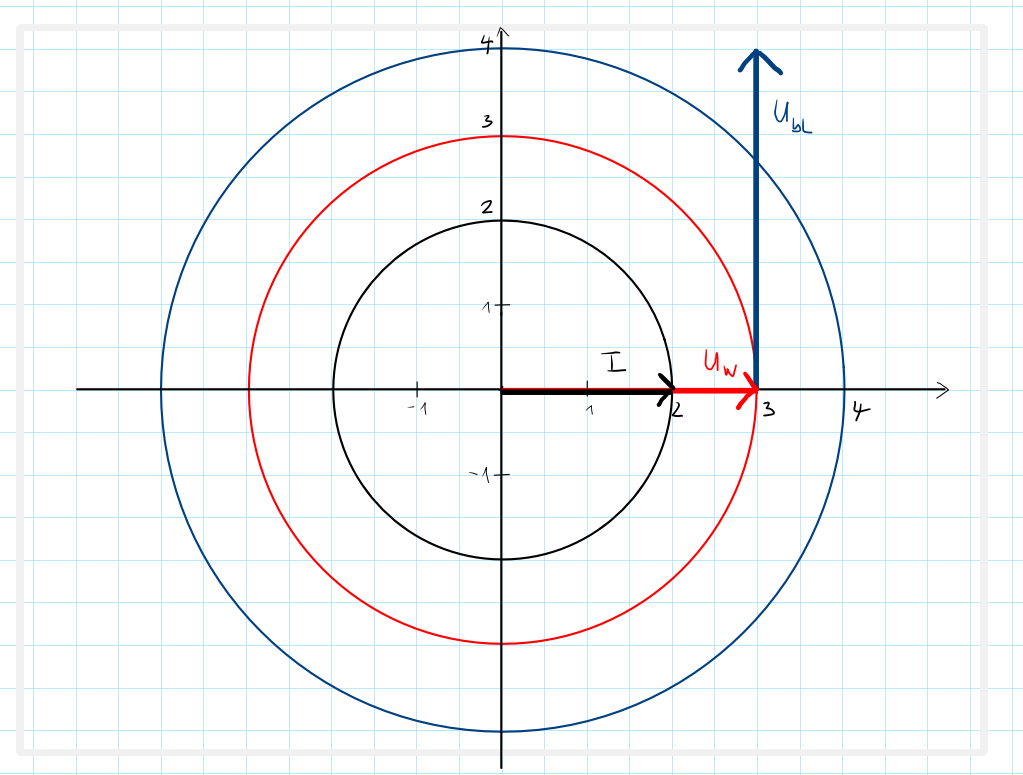
Anschließend wird der Anfang des Vektors \(U_W\) mit dem Ende des Vektors \(U_{bL}\) verbunden. Dies entspricht der Wechselspannung / Scheinspannung \(U\):
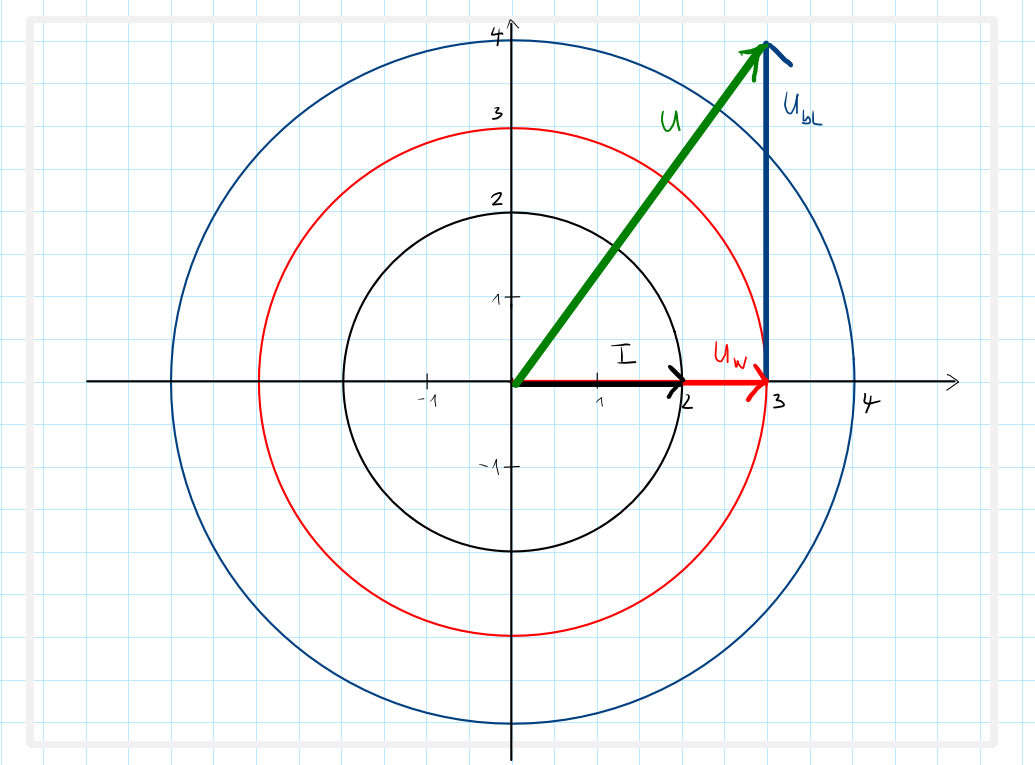
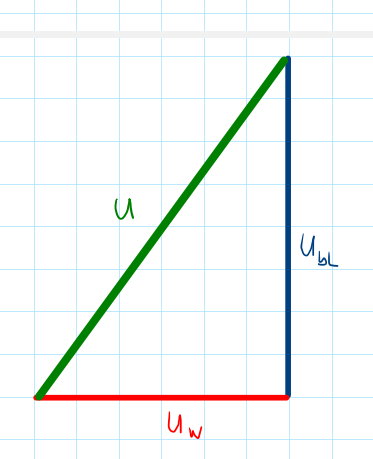
Entfernen wir nun die Kreise und den Strom, so erhalten wir ein Dreieck aus Vektoren:
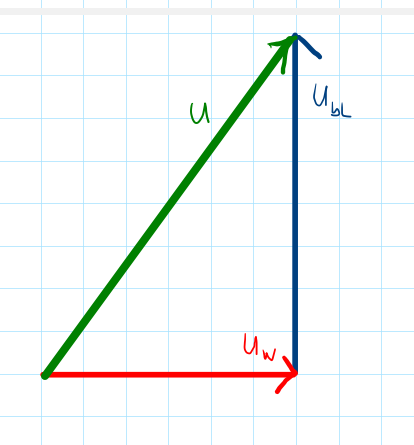
Abschließend werden aus den Vektoren die Seiten eines Dreiecks durch entfernen der Pfeilköpfe und wir erhalten das Spannungsdreieck:
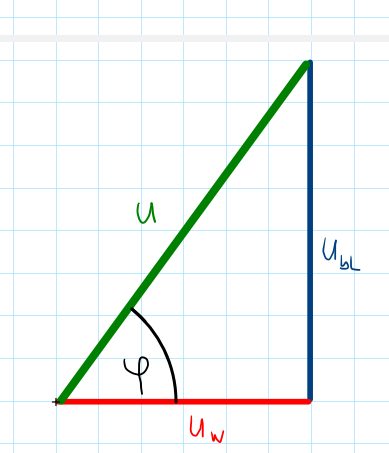
Zusatzinformation: Der Phasenverschiebungswinkel \(\varphi\) befindet sich zwischen der Scheinspannung \(U\) und der Wirkspannung \(U_W\):
Aufgabe 3
Ermittle eine Formel, mit welcher aus \(U_W\) und \(U_{bL}\) die Gesamtspannung ermittelt werden kann.
\(\sin(\varphi)=\frac{U_{bL}}{U}\Leftrightarrow U=\frac{U_{bL}}{\sin(\varphi)}\)
\(\cos(\varphi)=\frac{U_W}{U}\Leftrightarrow U=\frac{U_W}{\cos(\varphi)}\)
Aufgabe 4
Aus dem Spannungsdreieck läßt sich ein Widerstandsdreieck ableiten. Nutze die folgenden Formeln und berechne den Wirkwiderstand R und den induktiven Blindwiderstand \(X_L\).
Formeln: \(R=\frac{U_W}{I}\) und \(X_L=\frac{U_{bL}}{I}\)
\(R=\frac{U_W}{I}=\frac{3\ V}{2\ A}=1,5\ \Omega\)
\(X_L=\frac{U_{bL}}{I}=\frac{4\ V}{2\ A}=2\ \Omega\)
Aufgabe 5
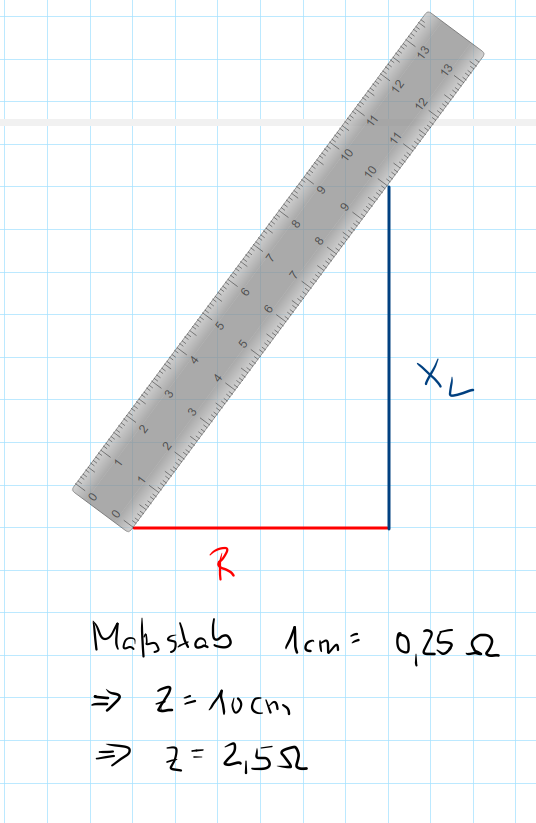
Zeichne ein Widerstandsdreieck mit den gefundenen Werten. Die entstehende Hypotenuse wird mit \(Z\) bezeichnet und gibt den Scheinwiderstand an. Nutze einen geeigneten Maßstab und miss den Scheinwiderstand.
Aufgabe 6
Finde eine Formel um den Scheinwiderstand \(Z\) aus dem Blindwiderstand \(X_L\) und dem Wirkwiderstand \(R\) zu berechnen.
\(Z^2=R^2+X_L^2\Leftrightarrow Z=\sqrt{R^2+X_L^2}=\sqrt{(1,5\ \Omega)^2+(2\ \Omega)^2}=2,5\ \Omega\)
Aufgabe 7
Zwischen Wirkwiderstand \(R\) und Scheinwiderstand \(Z\) liegt der Winkel \(\varphi\). Was gibt dieser Winkel an?
Die Phasenverschiebung zwischen Spannung und Strom.